[LeetCode][python3]0005. Longest Palindromic Substring
Start the Journey
N2I -2020.03.15
1. My first try
class Solution:
def longestPalindrome(self, s: str) -> str:
if not s:
return ""
elif len(s)==1:
return s
l=1
r=-1
max_sub=0
for i in range(1,len(s)):
cur_l,cur_r=self.lgcheck(s,i)
if r-l-1<cur_r-cur_l-1:
l=cur_l
r=cur_r
return s[l+1:r]
def lgcheck(self,s,start):
start_l=start-1
start_r=start+1
while start_l>=0 and start_r<len(s):
if s[start_l]!=s[start_r]:
break
else:
start_l-=1
start_r+=1
cur_max=start_r-start_l-1
r=start_r
l=start_l
start_r=start
start_l=start-1
while start_l>=0 and start_r<len(s):
if s[start_l]!=s[start_r]:
break
else:
start_l-=1
start_r+=1
if cur_max<start_r-start_l-1:
r=start_r
l=start_l


class Solution:
def longestPalindrome(self, s: str) -> str:
if not s:
return ""
elif len(s)==1:
return s
l=1
r=-1
max_sub=0
for i in range(1,len(s)):
cur_l,cur_r=self.lgcheck(s,i)
if r-l-1<cur_r-cur_l-1:
l=cur_l
r=cur_r
return s[l+1:r]
def lgcheck(self,s,start):
start_l=start-1
start_r=start+1
while start_l>=0 and start_r<len(s):
if s[start_l]!=s[start_r]:
break
else:
start_l-=1
start_r+=1
cur_max=start_r-start_l-1
r=start_r
l=start_l
start_r=start
start_l=start-1
while start_l>=0 and start_r<len(s):
if s[start_l]!=s[start_r]:
break
else:
start_l-=1
start_r+=1
if cur_max<start_r-start_l-1:
r=start_r
l=start_l


Explanation:
Just a normal solution for beginner.2. A better solution
class Solution:
def longestPalindrome(self, s: str) -> str:
str_len = len(s)
# if length of string < 2 or s is palindrome already
if str_len < 2 or s == s[::-1]:
return s
start, max_len = 0, 1
for i in range(1, str_len):
odd_start = i - max_len - 1
even_start = i - max_len
odd = s[odd_start:i + 1] # len(odd) = max_len + 2
even = s[even_start:i + 1] # len(even) = max_len + 1
if odd_start >= 0 and odd == odd[::-1]:
start = odd_start
max_len += 2
elif even_start >= 0 and even == even[::-1]:
start = even_start
max_len += 1
return s[start:start + max_len]
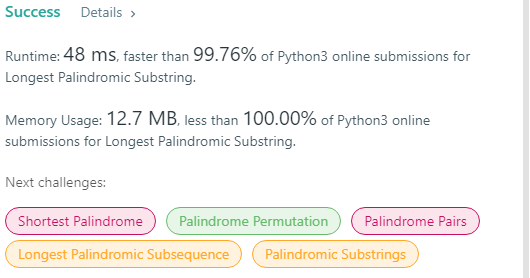
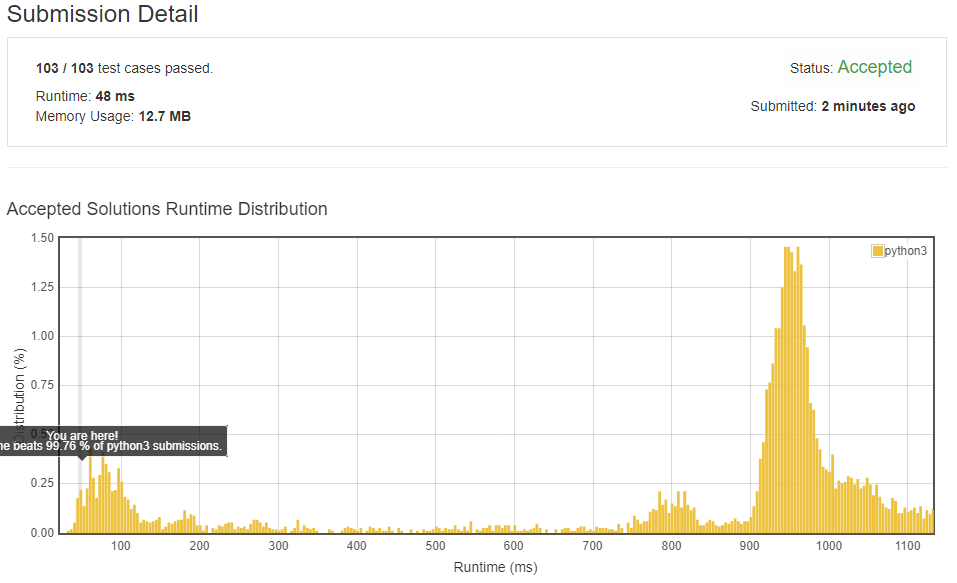
class Solution:
def longestPalindrome(self, s: str) -> str:
str_len = len(s)
# if length of string < 2 or s is palindrome already
if str_len < 2 or s == s[::-1]:
return s
start, max_len = 0, 1
for i in range(1, str_len):
odd_start = i - max_len - 1
even_start = i - max_len
odd = s[odd_start:i + 1] # len(odd) = max_len + 2
even = s[even_start:i + 1] # len(even) = max_len + 1
if odd_start >= 0 and odd == odd[::-1]:
start = odd_start
max_len += 2
elif even_start >= 0 and even == even[::-1]:
start = even_start
max_len += 1
return s[start:start + max_len]


Note:
even[::-1]is the reverse array foreven[:].s[a::b]is a sub_array of s,astands for the start index (default 0 or -1 whenb<0),bstands for what length for a jump.
print("note for s[a::b]")
print("while a stants and b>0")
s=[0,1,2,3,4,5]
s[::1]
>>>[0,1,2,3,4,5]
s[1::]
>>>[1,2,3,4,5]
s[1::2]
>>>[1,3,5]
s[1::3]
>>>[1,4]
s[2::2]
>>>[2,4]
print("while a <len(s) and b<0")
s[::-1]
>>>[5,4,3,2,1,0]
s[::-2]
>>>[5,3,1]
s[-2::-2]
>>>[4,2,0]
Explanation:
This solution use
even==even[::-1] to check the selecting area even=s[even_start,i+1]is palindrome or not. Since even or odd will always be 1 or 2 size longer then the current longest substring. start stands for the start of the current longest substring, will only changes when it finds a new longest one in odd or even.
Comments
Post a Comment